An Introduction to Algebraic Data Types

Structured, concrete data

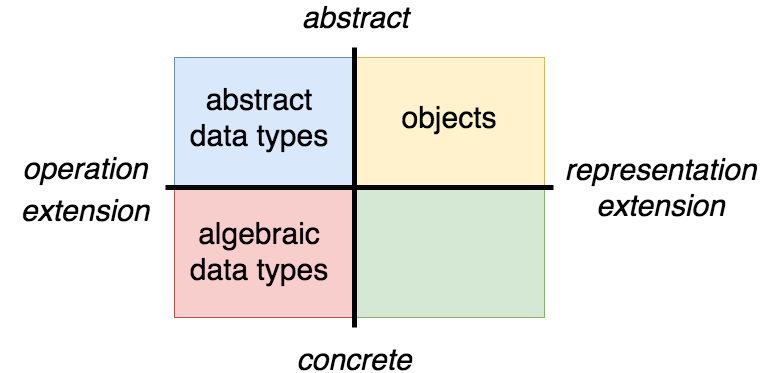
In my last post I said that there were three fundamental approaches to representing data: abstract data types, objects, and algebraic data types. I introduced abstract data types and objects (using a strict definition of “object” based on autognosis) and showed the tradeoffs of implementing data structures in these two styles. In this post I’ll introduce the third way to represent data, the “algebraic data type”, and show how its characteristics compare to those of abstract data types and objects.

Building up data #

Algebraic data types are the main method of representing data in ML family languages, like StandardML, OCaml, and Haskell. These languages have special syntax for working with algebraic data types, but this syntax is not necessary for them to be useful. All you need to use algebraic data types is a way to make constructors for pieces of data which can be distinguished from one another. In JavaScript we do this using class and instanceof. Here are implementations of two trivial algebraic data types, representing different kinds of fruit:

class Apple {}
class Blackberry {}

We can create instances of these data types using new: new Apple() or new Blackberry().

The reason these types are called “algebraic” is that we can create new types by taking the “sum” or “product” of existing types, just like we can make new terms of an equation by adding or multiplying existing terms in standard high-school algebra. To create a sum type, we’ll use |, meaning “or”:

type Fruit = Apple | Blackberry;

This says that we’ve added the Apple type to the Blackberry type to create the Fruit type. We can create a product type by combining existing types with a type constructor which takes multiple arguments:

class Pie {}
class Tart {}
class Dumpling {}

type Recipe = Pie | Tart | Dumpling;

class Dessert {
  fruit: Fruit;
  recipe: Recipe;
  constructor(fruit: Fruit, recipe: Recipe) {
    this.fruit = fruit;
    this.recipe = recipe;
  }
}

Here Recipe is another sum type, and Dessert is a product type formed out of Fruit and Recipe. To create a Dessert, we need to create instances of the types which it contains and then provide them to the Dessert constructor:

const appleTart = new Dessert(new Apple(), new Tart());

The names “sum” and “product” may be more intuitive if you think of the number of distinct values which exist of each type. The Apple constructor takes no arguments, and so (ignoring object reference comparisons) each instance of Apple is the same. This means that there’s one distinct value of the Apple type, and same for the Blackberry, Pie, Tart, and Dumpling types. The Fruit type adds together Apple and Blackberry, and so contains two distinct values, while Recipe adds together Pie, Tart, and Dumpling, and thus contains three distinct values. On the other hand, Dessert is a product of Fruit and Recipe, and thus contains six distinct values. Apple/Pie, Apple/Tart, Apple/Dumpling, Blackberry/Pie, Blackberry/Tart, Blackberry/Dumpling) Sum types add the number of possible values, product types multiply them.

This ability to create new types by combining previous types is essential to algebraic data types. There’s no limit to the composition of algebraic data types. Just as we created a Dessert type, we could createAppetizer and Entree types, and compose these three into a Dinner type. We could create Breakfast and Lunch types and compose them with Dinner to make a MealPlan type, etc.

Functions on algebraic data types #

Building up algebraic types is only half the story; to do anything useful with them we need to tear them down and look inside them. Most typed functional languages provide a special feature to do this (pattern matching), but in JavaScript we can do this using conditional logic and the instanceof operator.

To write functions on our sum types, we’ll break them into cases and provide a value for each member of the sum type:

function fruitToString(fruit: Fruit): string {
  return fruit instanceof Apple ? "apple" : "blackberry";
}

function recipeToString(recipe: Recipe): string {
  // prettier-ignore
  return recipe instanceof Pie  ? "pie"
  :      recipe instanceof Tart ? "tart"
  :      /* it's a Dumpling */ "dumpling";
}

The syntax on the second function may look strange, but it’s just one ternary expression nested inside another. When we nest ternaries like this, the conditions are checked from top to bottom, and the value that is paired with the first truthy condition will be the value of the overall expression. You can read functions written in this style like a table which provides an implementation of the function for each member of the sum type. (The bottom section of the MDN docs on the conditional operator also provides an introduction to this style.) Despite how useful this syntax is, the code autoformatter I use mangles it, hence the prettier-ignore comment.

Functions on product types are easier. They have access to all of the fields of the created type, without doing anything special:

function dessertToString(d: Dessert): string {
  return `a ${fruitToString(d.fruit)} ${recipeToString(
    d.recipe
  )}`;
}

Of course, just as we can compose as many algebraic data types as we want, we can also tear them down as far as we want. Here’s a function which digs two levels deep into its input:

function price(d: Dessert): number {
  // prettier-ignore
  return (  
    d.fruit instanceof Apple && d.recipe instanceof Pie ? 10  
  : d.fruit instanceof Apple && d.recipe instanceof Tart ? 4  
  : d.fruit instanceof Apple && d.recipe instanceof Dumpling ? 2  
  : d.fruit instanceof Blackberry && d.recipe instanceof Pie ? 12  
  : d.fruit instanceof Blackberry && d.recipe instanceof Tart ? 5  
  : /* we have a blackberry dumpling */ 3);
}

This is very different from abstract data types and objects, which both provide a small set of functions for operating on data while hiding that data’s internal structure. Algebraic types have the opposite intent: they provide a structure for data, to enable any number of functions to be written which work with that data.

A major benefit of algebraic data types is that the structure of algorithms which work on them tends to mirror the structure of the types themselves. Above we see that for a sum type with some number n members, functions consuming this type tend to have n cases. Though it’s not shown here, when an algebraic data type is recursive, functions consuming it tend to be recursive. (And functions consuming mutually recursive algebraic data types tend to be mutually recursive.) Algebraic data types can thus provide developers with guard rails when combined with a type checker, guiding the implementation of algorithms and ensuring that all possibilities are considered at each step.

One important characteristic of algebraic data types is that they should always be immutable. The examples of abstract data types and objects that I gave in the last post were immutable as well, but a mutable implementation would still have been valid by the definitions of “abstract data type” and “object”. By contrast, most languages which have algebraic data types do not support mutation of those types, or at the very least require special steps to make them mutable. When algebraic data types are used in languages where they aren’t particularly traditional, (like JavaScript) it would still be unusual and ill-advised to mutate them. Part of the nature of algebraic data types is that they work well with a mathematical and purely functional way of thinking about code. Mutating them would thus betray the expectations that developers usually rely on when working with them.

Comparing algebraic data types to objects #

For comparison’s sake, this is what an implementation of the above data structure using objects would look like:

interface HasName {
  getName(): string;
}

interface Fruit extends HasName {}

interface Recipe extends HasName {}

interface MenuItem extends HasName {
  getPrice(): number | null;
}

class Apple implements Fruit {
  getName() {
    return "apple";
  }
}

class Blackberry implements Fruit {
  getName() {
    return "blackberry";
  }
}

class Pie implements Recipe {
  getName() {
    return "pie";
  }
}

class Tart implements Recipe {
  getName() {
    return "tart";
  }
}

class Dumpling implements Recipe {
  getName() {
    return "dumpling";
  }
}

class Dessert implements HasName {
  private fruit: Fruit;
  private recipe: Recipe;
  constructor(fruit: Fruit, recipe: Recipe) {
    this.fruit = fruit;
    this.recipe = recipe;
  }
  getName() {
    return `a ${this.fruit.getName()} ${this.recipe.getName()}`;
  }
  getPrice() {
    const fruit = this.fruit.getName(),
      recipe = this.recipe.getName();

    // prettier-ignore
    return (
      fruit === "apple" && recipe === "pie"           ? 10
    : fruit === "apple" && recipe === "tart"          ? 4
    : fruit === "apple" && recipe === "dumpling"      ? 2
    : fruit === "blackberry" && recipe === "pie"      ? 12
    : fruit === "blackberry" && recipe === "tart"     ? 5
    : fruit === "blackberry" && recipe === "dumpling" ? 3
    : /* we don't know the price of this item     */ null);
  }
}

A few comments and notes of comparison on this implementation:

• Fruit and Recipe, which were sum types before, are now interfaces. In a realistic example these interfaces would have methods on them: maybe ways to query for the source of the fruit or its seasonality, or steps to cook the recipe. For simplicity’s sake all of the methods that are irrelevant to this example are omitted, and the interfaces are empty.
• Dessert, which was a product type before, still has the same internal structure and constructor signature. We’ve turned it from a plain container for holding data to an object with methods. To enable the kind of composability with hypothetical structures like Appetizer and Entree that were mentioned when discussing composition of algebraic data types, we’ve added a MenuItem interface and made Dessert implement it.
• The implementation of getPrice is interesting. It’s inherently a list of conditions, which associate arbitrary fruit/recipe pairs with a price. The principle of autognosis forbids us from using instanceof in an object implementation, so we use getName to differentiate the various fruits and recipes. This may seem like a violation of the spirit of autognosis, as we’re trying to determine what kind of object we’re dealing with. The difference here is that getName is a method on the object’s interface, which can be provided by any object implementing the Fruit interface. A user could create different kinds of Apple, such as GalaApple or HoneyCrispApple, which still return "apple" from getName but differ in other ways. These different objects could be passed to Dessert, and Dessert’s getPrice method would still work. This technique of imitating another object is often called “impersonation”. The fact that arbitrary additional implementations can impersonate our objects is an essential aspect of an object-based approach’s extensibility.
• The signature of getPrice has changed. In the algebraic data type implementation, it returned a number, but now it returns number | null. This is because in the algebraic data type implementation, all of the possibilities are listed in the type signatures of our sum types and we can be sure that our implementation covers every possible combination. The open extensibility of objects comes with a cost: We have no way to guard against someone adding a new Fruit type which returns "orange" from its getName method and then asking us for the price of an orange pie. (Which we cannot provide.) We need to add an error case to our return values to handle unexpected cases like this.

This last point shows the “guard rails” provided by algebraic data types in action. Because our sum types are an exhaustive list of possibilities, consuming a sum type in a function just requires writing a case for every member of the sum, and gives us the guarantee that we aren’t missing any possibility. This lets us dodge edge cases like the possibility of missing prices in the object implementation.

If we think of the members of a sum type as “representations” of that type, in the same sense that classes provide different representations of an interface, we can see that algebraic data type’s representational extensibility is very limited. Consider adding a new Fruit to each implementation above. Adding a new option to a sum type requires updating every function which consumes that type and adding a conditional and case for the new member. This is the cost of the guarantees and guidance that having an exhaustive list of possibilities gives us: our functions are tightly coupled to the data which they run on.

By comparison, adding new operations to an algebraic data type is quite easy. Operations are defined as functions, completely separately from the data type’s type signatures and constructors. Anyone, anywhere can add new functions which consume or return an algebraic data type.

Algebraic data types thus give up easy representational extensibility in exchange for great operational extensibility. I mentioned that this tradeoff is called the “expression problem” when I introduced objects. Just as more advanced techniques can enable objects to overcome this tradeoff, offering modular extension on both fronts, so too can more complex usages of algebraic data types. As with objects, solutions which provide both kinds of extensibility are much more involved than the easy approach that we have here.

Algebraic data types have a more complex set of tradeoffs with respect to performance than objects do. One of the costs of object’s extensibility was a greatly reduced potential for optimization. Autognostic solutions do not have an accessible structure, and so optimization techniques which reduce a large structure into a smaller one face serious limitations when applied to objects. Algebraic data types excel on this front; because their structure is not abstracted, any function which operates on them has the option to make whatever simplifications may be desired. On the other hand, because objects can be mutable and algebraic data types should not be, optimizations which rely on mutation are available to objects but not to algebraic data types.

Comparing algebraic data types to abstract data types #

The tradeoffs provided by algebraic data types are very similar to those provided by abstract data types; both are extensible operationally but not representationally. In fact, every algebraic data type can be trivially used as an abstract data type. All that’s needed is to export functions for working with the algebraic type and functions for creating them, but hiding the constructors and the type definitions themselves. This conversion does not go both ways; abstract data types cannot be used as algebraic data types, because algebraic data types have the strict rule that they’re implemented purely as nested constructors and should be immutable, while abstract data types often take advantage of different language features.

Despite their similarities at a high level, there are important distinctions between these two:

Algebraic types have much better public operational extensibility. Only operations which are defined within an abstract data type’s module have access to that type’s internal structure, limiting the functions which developers consuming the type can implement on it. By contrast, the concreteness of algebraic data types means that consumers have all of the same capabilities for working with them as do the authors of a module that exports them.

Abstract data types have a great deal of freedom to evolve their implementation over time, while this evolution with algebraic data types is much more involved. This is the benefit of hiding their internal structure from consumers; an abstract data type can have its internal structure completely rewritten without breaking consumers. In contrast, once an algebraic data type is published, any change to that type’s structure is a breaking change. This can be a good thing; after modifying an algebraic data type, a type checker can assist in locating the code which will be affected by that change. Nevertheless, the rippling of these changes through a codebase is a distinct cost of using a non-abstract solution.

Finally, as mentioned in the previous section, optimizing immutable data structures presents more challenges than optimizing mutable ones. This means that abstract data types have easy access to a host of optimization techniques which algebraic data types do not. This does not mean that algebraic data types are slow; many efficient data structures exist as algebraic data types and there are resources for learning how to design and think about them. It does mean, though, that optimizing complex algorithms on novel data types can be more challenging when working with immutable algebraic data types than with mutable abstract data types.

This concludes our tour of basic approaches to representing data. In the first post we saw abstract data types and objects, two approaches to data abstraction which take opposite sides on the operational extensibility/representational extensibility tradeoff. Algebraic types are fundamentally different, in that they do not provide any abstraction at all, and instead provide a structure which guides the implementation of any functions which consume them. Algebraic data types are very operationally extensible, even more so than abstract data types, because all consumers have access to their structure and can implement arbitrary logic to manipulate them. They have poor representational extensibility, though, and any change to their structure is a breaking change for consumers. Algebraic data types are the approach of choice for most typed functional languages, and their immutability, composability, and known structure make them a great choice when approaching problems functionally.

This post is a reworking of one which I originally published on Medium. You can view my old Medium posts here.